Lehrgang zum geometrischen Freihandzeichnen

Um geometrisches Freihandzeichnen im Unterricht zu einem brauchbaren Werkzeug unter Beachtung der Zeitökonomie zu machen, ist eine systematische Einführung unerlässlich. Der Autor hat beste Erfahrung mit kurzen und zeitversetzten Sequenzen, die in der Bearbeitung einiger weniger Kopiervorlagen bestehen, gemacht. Diese benötigen jeweils nur wenige Minuten je Unterrichtsstunde. Vom Inhalt her können sie schon sehr frühzeitig, am besten zu Beginn der Sekundarstufe eingesetzt werden.

Für die Zeichenpraxis sei auf den Menüpunkt „Hinweise und Tipps“ verwiesen.

Durch die Bearbeitung der folgenden Blätter wird schrittweises Bekanntmachen mit den elementaren Regeln, die sich aus der Zeichenpraxis heraus entwickelt und als vorteilhaft erwiesen haben, gewährleistet.
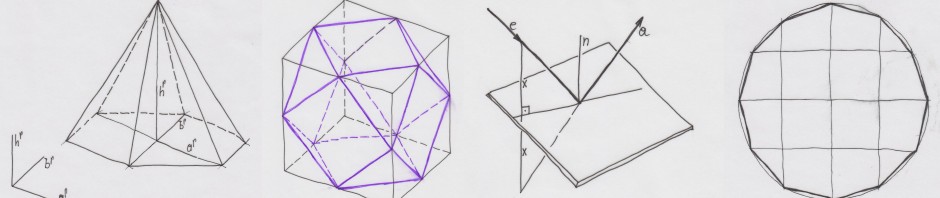
Bei den Lehrerfortbildungskursen konnten in kurzer Zeit (in etwa 3 – 5 Einheiten á 45 Minuten) alle TeilnehmerInnen ein solches Niveau erreichen, dass sie selbst komplexe geometrische Konstruktionen (etwa Kugeldarstellung samt Schnittkreisen in Normalrissen, Perspektiven technischer Objekte, Platonische Körper …) sehr rasch darstellen konnten.
Die ersten vier Blätter dienen der handwerklichen Einführung in das geometrische Freihandzeichnen: Konzentration und Linienführung sind die Schwerpunkte – kein Radieren zulassen, damit die Schülerinnen und Schüler die Furcht vor krummen und verwackelten Linien überwinden. Die weiteren Blätter bieten die Möglichkeit der Vertiefung der Kenntnisse in ebener Geometrie (regelmäßige Vielecke) oder eines Einstiegs in die Raumgeometrie.

Hinweis: Zum Download der Kopiervorlagen klicken Sie zunächst mit der linken Maustaste auf die Vorschaubildchen. So erscheint das Bild in Originalgröße. Danach mit der rechten Maustaste auf das nun erschienene Bild. Im entstehenden Menü wählen Sie „Bild speichern unter“ aus.

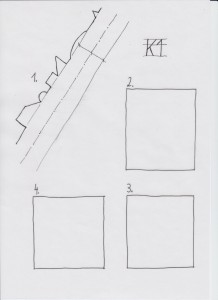
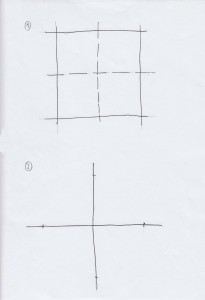
Kopiervorlage 1: Strichübungen/Zeichentechnik Strichbreite, Strichstärke

Aufgabe 1: Der Streckenzug soll zunächst zügig nachgezogen werden – ohne abzusetzen. Dies stellt eine gewisse Anforderung an die Konzentrationsfähigkeit dar. Anschließend zeichnet man den an der strichliert vorgegebenen geraden Linie gespiegelten Streckenzug. Achten Sie auf einen gleichmäßigen Grauwert und gleichmäßige Strichstärke.
Aufgabe 2: Waagrechte Seiten des Rechteckes halbieren, die entstehenden Hälften nochmals halbieren (vgl. Bemerkungen bei Abb. 16), die Teilungspunkte der oberen Seite werden mit den korrespondierenden der unteren Seite freihändig verbunden, sodass Parallele zu den linken und rechten Seiten entstehen: Dabei besondere Beachtung exakt ausgeführter Endpunkte – kein Überfahren von vorgegebenen Grenzen.
Aufgabe 3: Hier sollen die lotrechten Rechteckseiten analog zu oben geviertelt und die Teilungspunkte dann entsprechend verbunden werden.
ACHTUNG: Zunächst wird das Blatt um 90° gedreht, damit der Zeichner/die Zeichnerin dieselbe Situation wie bei Aufgabe 2 vorfindet.
Aufgabe 4: Nun werden beide Übungen nochmals – aber in ein und demselben Rechteck durchgeführt.

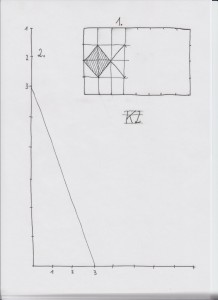
Kopiervorlage 2: Zeichnen längerer„gerader“ Linien, Zielübungen

Aufgabe 1: Bei den Rechteckseiten sind Teilungspunkte vorgegeben, die Teilstrecken sind annähernd gleich lang. Durch Verbindung gegenüberliegender Punkte entsteht ein Quadratraster. (Vergessen Sie nicht, das Blatt wieder um 90° zu drehen!) Danach soll eine parallele Linienschar in einer Diagonalrichtung eingetragen werden. Dass die Diagonalparallelen nicht alle Quadratrasterpunkte genau treffen werden, muss akzeptiert werden. Gerade dieser Umstand kann den Bogen hin zur geometrischen Überlegung schließen und die Beweisbedürftigkeit dieser Tatsache steigern.

Aufgabe 2: Es geht um das Zeichnen langer Linien, die annähernd gerade sein sollen. Beachten Sie dabei besonders Tipp 4 im Infofenster 5! Die beschrifteten Punkte sollen im Sinne aufsteigender Zahlen durch Strecken verbunden werden. Hierbei soll das Ziehen der Linien „zum Nabel hin“ eingeübt werden.

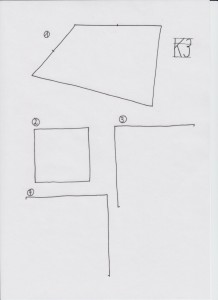
Kopiervorlage 3: Abstandsübungen, Halbieren, Teilen von Strecken

Einfache mathematische Sätze können zu diesem Zeitpunkt „nebenbei“ entdeckt werden: Aufgabe 1: Die Halbierungspunkte der vier Seiten des gegebenen allgemeinen Vierecks bilden ein neues Viereck, welche einzutragen ist. Scheint dieses Viereck rein zufällig ein Parallelogramm zu sein? Das Eintragen der Diagonalenstrecken des gegebenen Vierecks kann die Beweisüberlegung in bekannter Weise vorbereiten. Auch der Satz von der Winkelsumme eines Vierecks kann in diesem Zusammenhang erläutert/wiederholt werden.
Aufgabe 2: In das Quadrat werden analog zur Aufgabe 1 die Halbierungs-punkte der Seiten samt entstandenem Viereck (Quadrat) und die Diagonalen eingetragen.
Aufgabe 3: Nach der Ergänzung zu einem Quadrat werden die Seiten geviertelt. Durch die Verbindungslinien der jeweils an den Eckpunkten anliegenden Teilungspunkte werden die Ecken des Quadrates gleichsam abgeschnitten. Es entsteht ein Achteck. Dass es nicht regelmäßig ist, ist evident (Seitenlängenvergleich!).
Aufgabe 4: Nach der Ergänzung zu einem Quadrat und Eintragen der Diagonalen werden die halben Diagonalstrecken des Quadrates auf deren Seiten von jedem Eckpunkt aus abgetragen. Dies kann etwa mit einem Lineal oder „freihandgemäßer“ mit angelegten Papierstreifen geschehen. So hat man acht Punkte erhalten. Dass dieses Achteck ein regelmäßiges ist, kann man durch Seitenlängenvergleich sehen.
Nach Durchführung dieser Übungen kann man – wie oben angekündigt – je nach Klassenstufe und/oder Intention des/der Lehrenden weiter in der ebenen Geometrie bleiben oder in die Grundzüge der Darstellung räumlicher Objekte einsteigen. Die Einstiegskopiervorlagen seien jeweils angegeben.

Möglichkeit 1 / Ebene Geometrie

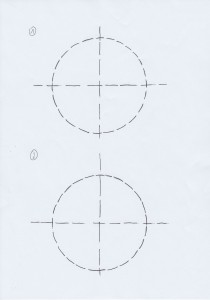
Kopiervorlage 4: Kreise zeichnen
Viebahn beschreibt zwei unterschiedliche Möglichkeiten, freihändig Kreise zu zeichnen, zum einen mit Hilfe eines umschriebenen Quadrates und zum anderen mit Hilfe von Radien (vgl. auch Tipp 6 im Infofenster 5). Diese Vorlage könnte, falls die Unterrichtszeit nicht ausreicht, übersprungen werden. Statt dessen könnte mit vorgegebenen oder mit Hilfe eines Zirkels gezeichneten Kreisen (Kopiervorlage 5) weitergearbeitet werden.

 

 

Kopiervorlage 5: Teilung von Kreisen/regelmäßige Vielecke

Durch Teilungen der Radien könnte ein regelmäßiges 12-Eck erzeugt werden, durch Eintragung der Winkelsymmetralen der normalen Kreisdurchmesser ein regelmäßiges Achteck, durch Abtragen der Radien mit Hilfe eines angelegten Papierstreifens ein regelmäßiges Sechseck usf.

 

 

 

 

 

Möglichkeit 2 / Raumgeometrie

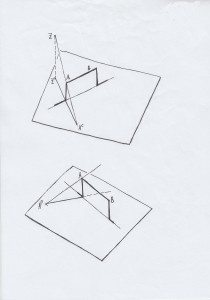
Kopiervorlage 6: Elementares zur Parallelprojektion und Zentralprojektion

Durch die Vervollständigung der vorgegebenen Skizzen lassen sich die wichtigsten Eigenschaften der Parallelprojektion und der Zentralprojektion vergleichend erarbeiten. (Vergleiche hierzu auch im Abschnitt Freihandzeichnen und Computereinsatz die Hinweise zu These 5.)

 

 

 

 

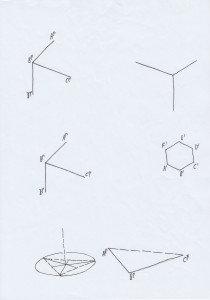
Kopiervorlage 7: Würfel, Prisma, Pyramide

In dieser Vorlage werden lediglich die Eigenschaften der Parallelentreue und Mittelpunktstreue benötigt. So lassen sich damit die drei vorgegebenen Kantenbilder im ersten Beispiel etwa zum Bild des Kantenmodells eines Würfels, im zweiten Beispiel zum Bild eines regelmäßigen sechsseitigen Prismas ergänzen. Im dritten Beispiel soll über dem Bild eines gleichseitigen Dreiecks eine Pyramide errichtet werden. Der Höhenfußpunkt als Bild der Umkreismitte kann im Bild nur unter Beachtung der Mittelpunktstreue gefunden werden, fällt doch der Schwerpunkt im vorliegenden Dreieck mit dem Umkreismittelpunkt zusammen.